 |
An elegant Object Oriented C++ library for arbitrarily large integer numbers and arbitrarily precise rational numbers. |
| Open Source License |
| Before using the Proper Numbers Library you must agree with the Software License. |
| Synopsis |
|
The Proper Numbers Library is a small, efficient and fast set of C++ classes which allows representation of arbitrarily large integer numbers, arbitrarily precise rational
numbers and quadratic-like irrational real numbers in a natural way. The classes are defined in header files only, and so it is only necessary to include these header files
in the h/cpp files of a project (and if required, to add them to the project) to have the library up and ready to use.
|
| History and Background |
| Why was the Proper Numbers Library created? |
As a final year student in mathematics, I had to produce an MSci dissertation project. The name of the project that I chose was the Mean Median Map. The Mean Median Map
is a recursive function which appears to have very complex behavior and spectacular dynamics, but in fact it is a very simple function.
The nature of the problem is such that if one is to emulate the map, they need an absolute precision in all computations. Since the floating point numbers usually used for
computations are not precise and I needed to emulate the map in order to see its behavior in different circumstances, I created the Proper Numbers Library with the desired
properties. The Proper Numbers Library uses the Object Contextualization Model which I developed separately in late 2009,
but I never had the time to write a paper on it and publish it. However, since I have used it in the Proper Numbers Library, I thought it best to describe and publish it.
Thus the Mean Median Map project brought forward three very good results: 1) explained the nature of the map;
2) the Proper Numbers Library; 3) made me finally publish the Object Contextualization Model.
In my view, the most interesting part of the Mean Median Map project for both computer scientists and mathematicians is the fact that the sole reason that allowed me to understand
how the map works was my constructivist view of the world which was enforced by computer science. In this project, Computer Science and Mathematics are complementary to each other
and the product of that beautiful marriage was that the nature of the map was explained. For the record, I do not find it appropriate to separate Computer Science from Mathematics,
I think that they are one and the same thing. If you cannot read the document please: click here.
|
|
|
|
| The Mean Median Map software application, is included as an example project using the Proper Numbers Library. |
| Why is the Proper Numbers Library called "Proper"? |
| Integer Numbers:
As you probably already know, computers work with fixed size binary fields called registers. These registers tend to overflow in some cases, and when this happens,
the number they hold most likely becomes wrong, i.e. not representing the value it should, unless of course if the software in fact represents the right type of
modular arithmetic. The latter is not very usual at all, so usually developers have to always make the correct choice in setting the size of their variables so
that they do not overflow. In fact, computers always work in modular arithmetic Z28, Z216,
Z232 or Z264 depending on the registers that are being used, and developers usually want
to keep the calculations and the numbers they work with within one partition and subgroup of Z. When working with assembly languages, developers can
check for various carry and overflow flags that the processor sets when overflows occur, but these are lost when working with high-level languages. To summarize, the
problem with integers in computers is that they wrap up, so we can say that integers in computers are not exactly proper as they are in fact modular integers.
|
| Real Numbers:
The floating point numbers in computers are an attempt to represent the Real numbers ℜ, and thus in some languages they are called REAL as opposed
to float or double in others. The floating point numbers have more drawbacks than advantages. The only advantage that they have is that they
are easy to work with, and when a machine is equipped with a mathematical coprocessor, which is the case for most modern computers/processors, they can be very fast to compute
with. The disadvantages that they have are that they do not represent all numbers, even within the range on which they are defined. Floating point numbers also have very
irregular distribution on the number line. They are denser near the zero and further away from each other as moving away from the zero. In fact the floating point numbers
are nothing more than a poor set of irregularly distributed rational numbers in exponential notation. Further, because of their incompleteness, they introduce accumulative
rounding errors which are dependent on the actual numbers being computed. In other words, floating point numbers are a very bad choice when precision is essential. There are
also significant problems with the definition of the real ℜ numbers, and therefore with their REAL/double floating point representatives. Real numbers are supposed to
present a continuum, which of course for a computer scientist is an absolute nonsense. Real numbers are defined in two ways. The first way is axiomatically - one just decides
to believe in them. Well, I decide NOT to believe in them because there are more and better reasons to believe that the world is discrete. The second way for defining the Real
numbers is by converging infinite Cauchy sequences, which in brief says that if one is to add infinitely many rational numbers, in particular cases you will end up with a Real
number. Of course, that is not plausible for computer scientists since operator on rational numbers always returns rational numbers, and infinity does not matter in the slightest.
It does not matter how many times a rational operator is applied - it will always return a rational number since it is defined in such a way. Secondly, applying an operation infinitely
many times is possible only in one's imagination, but not in any reality. Thirdly, infinity does not exist,
and therefore neither does continuum, nor do Real numbers, regardless of attempting to define them axiomatically or by infinite Cauchy sequences. In short, for computer scientists,
real numbers in general are things that are in fact impossible to believe in. Of course Real ℜ numbers, being unreal, are also never used in practice. In
practice, people always work with rational numbers with some appropriate precision - always rational - be it to fly an aircraft, build a microprocessor chip or whatever else. To
summarize, the problem with floating point numbers in computers is that they are very few, they are imprecise and they are very much distorted, so we can say that floating point
numbers are not exactly proper.
|
| Irrational Numbers:
Irrational numbers are not present in computers at all. The Proper Number Library makes an attempt to present them in the form of a Quadratic-like family of numbers. Thus, numbers
such as √2 are presented in the form: a ± fun( b ), where a, b ∈ Q and fun is a function such that fun-1 exists.
However, there are some problems with the model. Irrational numbers are very rarely used in general software development as computations are normally carried out numerically and
not symbolically. Although there are problems with the definition of the irrational numbers in the Proper Number Library, they are sufficiently well-defined for the purposes of the
Mean Median Map and it is likely that this is also true for most other purposes that they might be required for. However, a proper investigation on the problem is required.
|
| The library is called proper because: |
| 1. It works with truly existing numbers - the Integer and the Rational numbers. |
| 2. The numbers are able to expand arbitrarily. (Any existing number that exists in the Universe of Discourse (assuming a discrete world) is representable (up to available memory)). |
| 3. The numbers are well behaved and evenly distributed. |
| 4. The library is small and very efficient. |
| Arbitrarily Large Integer Numbers Class |
The Integer class represents unsigned integers with arbitrary precision. Objects from this type expand arbitrarily large up to available
memory and are able to accommodate arbitrarily large numbers (up to the available memory).
Integers in a digital computer are manipulated by bit fields called registers able to do bitwise operations and operations on the whole field, such as ADD (add),
ADC (add with carry), SUB (subtract), AND (and), OR (or), etc. These are called instructions. There are a number of flags in the processor's Control and Status
register that signal or indicate about different conditions that may have occurred. For example, overflow after an addition operation. Depending on the number of
bits in the register, it is a variable of type Z2number-of-bits usually Z28,
Z216, Z232, Z264 and operate in the respective
modular arithmetic. High level languages utilize the processor registers to perform arithmetic and other operations on the content of the memory. Integer variables
in high level languages are byte arrays with sufficient size located in the memory and are designated with its name in the metaspace. When an integer variable is
larger than the largest register able to perform integer operations, the compiler/assembly programmer typically uses a loop and the status flags applying the operation
throughout the whole array working in Z2number-of-bits-in-variable. Thus if a variable is 128 bit (16 bytes) and the largest
arithmetic register is 16 bit, the compiler will place a function call for every arithmetic operation on the variable. There will be a loop from 1 to 16 iterations
in the body of function using appropriate processor instructions on only 16 bits (2 bytes) at a time, achieving correct results in Z2128.
The Integer class from the Proper Numbers Library uses a similar approach, but instead of using constant size arrays to represents integers, it uses a generic linked list.
Each number is composited from one or more 64 bit words. Arithmetic operations are implemented using a set of appropriate fast algorithms. When the operation is about to
produce a number with a greater size then the current one, it is carried out and adds more space to the number and thus overflows do not occur. Hence the integer class represents
N (up to the available memory in the system). Shift to right and subtraction decrease the size of the number (object). Empty number is not allowed. Zero is
represented with one 64 bit word set to zero. The Integer objects are maintained normalized, which for this class means that there are no leading zeroed 64 bit words -
except for the one zero word for the 0. When subtracting a larger number from a smaller one, the result wraps up and has the size of the larger number. The decrement operator
has an unusual behavior - it does NOT decrement below zero to avoid ambiguity.
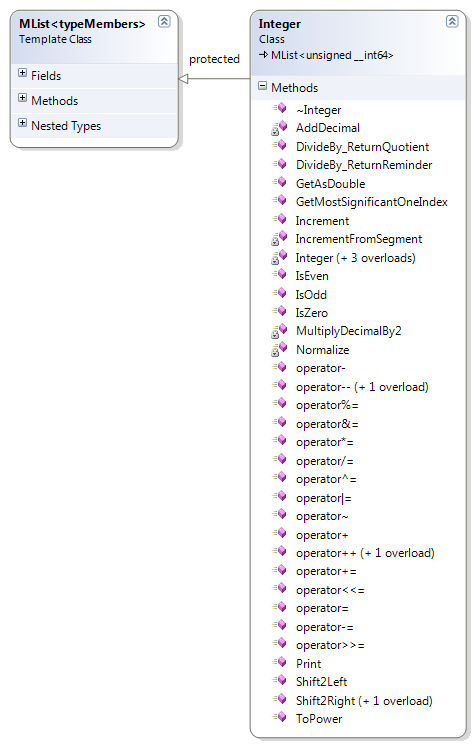
Remarkably, the Integer class is a specialization of a linked list of type MList< unsigned __int64 >. When a number is represented with an
object of this type, the underlying linked list is accelerated and thus the words of the number are accessed as an array, achieving performance as if the numbers were indeed
represented by an array. The integer class inherits the list as protected access and thus the methods of the underling list are not visible (accessible) from an integer instance.
Integer objects throw NumberException only when dividing by zero. This behavior may change in future, removing all exceptions altogether (though this is not likely), or a new
operator with an alternative behavior may be provided. The division operator returns a specialized Quotient and Reminder pair, thus helping to prevent errors.
The Boolean operators are NOT overloaded purposefully. The reason is that Integer numbers are NOT Boolean entities and therefore they should not implicitly represent Boolean values.
Should one want to use them as Boolean variables, they can use the IsZero() method and the comparison operators appropriately.
Objects from the Integer class are able to print themselves using the Print() method.
Remark. The Integer class represents N and not Z purposefully. This is necessary to maintain a correct model without redundancies. Signed integers
Z⊂Q can be represented using rational numbers with denominator 1. Otherwise there would be redundancies in the sign and computation of every rational
number, which is a clear and definitive indication of an inconsistent model.
|
|
|
|
|
This class uses a number of general purpose classes, such as linked list, string, memory atom, pair and others, available to download with the Proper Numbers Library.
|
| Figure 1. Class diagram of the Integer class. |
An example of how to use the Integer class: |
|
VOID _tmain( INT argc, _TCHAR* argv[] )
{
Integer a( 3 );
Integer b( 2 );
Integer c( 3452 );
wprintf( TEXT("%s\n"), (LPCTSTR)c.Print() );
c += b;
wprintf( TEXT("%s\n"), (LPCTSTR)c.Print() );
Integer d = a * b + c;
wprintf( TEXT("%s\n"), (LPCTSTR)d.Print() );
c--;
wprintf( TEXT("%s\n"), (LPCTSTR)c.Print() );
b--;
wprintf( TEXT("%s\n"), (LPCTSTR)b.Print() );
}
For more examples please see the Mean Median Map project.
|
|
| Arbitrarily Precise Rational Numbers Class |
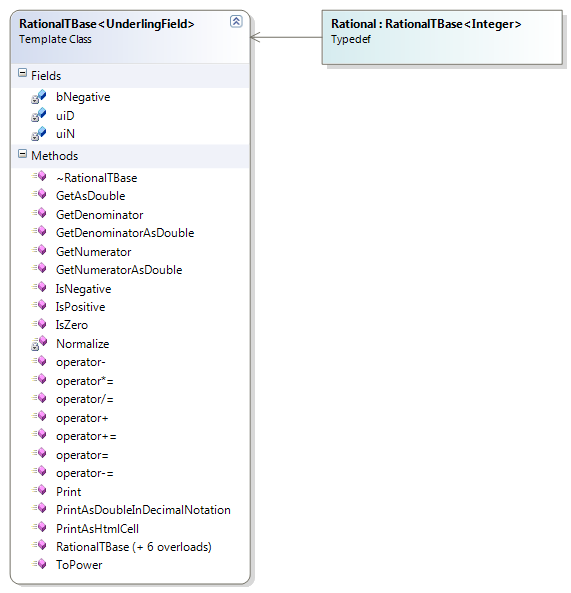
The RationalTBase template class represents rational numbers over an unspecified specializer which must be at least a commutative ring with identity (CRI).
A rational entity is constructed by a sign and an ordered pair of numerator and denominator. The objects are always normalized, i.e. the numerator and
denominator are always coprime. When RationalTBase is specialized with the Integer class (which represents N (up to available memory)) the
resulting type represents Q (up to available memory), i.e. the objects of type RationalTBase< Integer > are rational numbers with arbitrary
precision and even distribution, thus they are perfect for precise computations. It is possible to use other types of underlying CRIs, such as unsigned char
- Z28, unsigned short - Z216, unsigned int - Z232,
unsigned long - Z232, unsigned __int64 - Z264, etc. or applicable user-defined types.
Being a commutative ring with an identity, the specializer is expected to have all appropriate operators defined.
The behavior of the type is determined by its own nature and also by the behavior of the underlying CRI. For example, overflows (when applicable) may or may not be
signaled depending on the behavior of the underlying ring. RationalTBase throws NumberException only when dividing by zero. This behavior may change in future removing
all exceptions altogether (though this is not likely), or a new operator with an alternative behavior will be provided.
Boolean and bitwise operators of RationalTBase are NOT overloaded purposefully. The reason is that rational numbers are not Boolean or bit-field entities and
therefore should not implicitly represent them. Objects from the rational class are able to print themselves in various ways.
The Rational is a type definition, specialization of RationalTBase with the Integer class representing arbitrary precision rational numbers. It is ideal for use when
precise computations are required. The Rational is a commutative ring with identity (CRI) with all appropriate operators and thus can be used whenever CRI is needed.
|
| The RationalTBase Template Class and Rational Specialization |
|
|
|
|
This class uses a number of general purpose classes, such as linked list, string, memory atom, pair and others, available to download with the Proper Numbers Library.
|
| Figure 2. Class diagram of the RationalTBBase template and Rational specialization. |
An example of how to use the Rational class: |
 |
VOID _tmain( INT argc, _TCHAR* argv[] )
{
Rational a( 2, 3 );
Rational b( 3, 4 );
Rational c( 7, 2 );
Rational d( -5 );
Rational e = ((a + b ) * c) / (d - 456 * c);
wprintf(TEXT("e=%s; e(as floating approximation)=%.16f\n"),
(LPCTSTR)e.Print(), e.GetAsDouble());
}
Result:
e=-(119, 38424); e(as floating approximation) = 0.0030970226941495
For more examples please see the Mean Median Map project.
|
|
| Irrational Numbers Template Class |
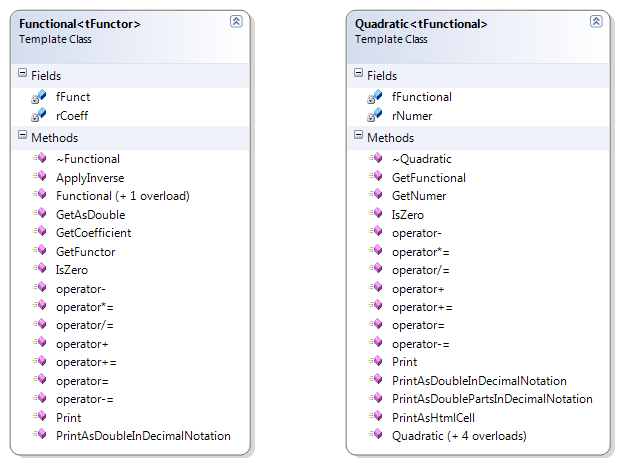
The quadratic irrational template represents a Quadratic-like family of Real numbers. The class consists of a Rational and a Functional element. The functional is a template
on its own, specialized with the specializer of the quadratic template. The quadratic specializer is propagated onto the functional and is not otherwise used by the quadratic
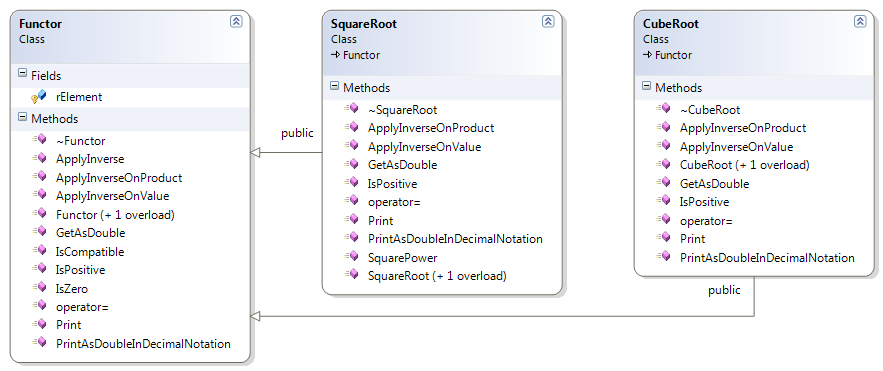
type. The functional expects to be specialized with a class derived from an abstract class called Functor. The Functor represents a real function with a rational variable.
The functor is defined as an abstract class, as follows:
Functor( x ) := f( x ), where x ∈ Q, f is a Real function.
The Functional is defined as:
Functional( Functor( x ), y ) := yFunctor( x ), where y ∈ Q.
The Quadratic is defined as:
Quadratic( Functional( Functor( x ), y ), z ) := z + Functional( Functor( x ), y ), where z ∈ Q.
Thus the definition of quadratic number is q = z + yf(x), where
x, y, z ∈ Q and
f is an unspecified real function with inverse. In particular
f could be defined as
f := √x,
f := 3√x, or any other real function with one variable.
Problem. The Quadratic template definition appears consistent; however it is impossible to have default constructor on the Quadratic since the
variable under the functor cannot be predefined. Thus one or more of the following is true:
1. The declaration above meets the requirement and represents the required irrational numbers, however it is inconsistent in general, i.e. non bijective.
2. It is not possible to have more than one under-functor-variable per universe.
3. Default constructor is not necessary to exist.
4. There is a fundamental problem with quadratic numbers definition or numbers in general.
Irrational numbers are very rarely used in general software development as computations are normally carried out numerically and not symbolically. However,
this problem is clearly complex and serious, and requires an investigation of its own. The Quadratic template, as defined above, was sufficiently consistent
for the Mean Median Map investigation and was successfully used in it; however the problem is extremely interesting and deserves further research.
|
| The Quadratic Template Class |
|
|
|
|
This class uses a number of general purpose classes, such as linked list, string, memory atom, pair and others, available to download with the Proper Numbers Library.
|
| Figure 3. Class diagram of the Functional and Quadratic template classes. |
 |
| Figure 4. Class diagram of the Functor abstract class and two derived from it functors. |
 |
| An example of how to use the Quadratic class: |
VOID _tmain( INT argc, _TCHAR* argv[] )
{
Quadratic< SquareRoot > q1( Rational( specialize< Integer as sX::Numerator >( specialize< Integer as sX::Numerator >::Initialize( 1 ) ),
specialize< Integer as sX::Denominator >( specialize< Integer as sX::Denominator >::Initialize( 2 ) ) ),
Functional< SquareRoot >( 3, SquareRoot( 5 ) ) );
Quadratic< SquareRoot > q1( Rational( specialize< Integer as sX::Numerator >( specialize< Integer as sX::Numerator >::Initialize( 1 ) ),
specialize< Integer as sX::Denominator >( specialize< Integer as sX::Denominator >::Initialize( 7 ) ) ),
Functional< SquareRoot >( 7, SquareRoot( 5 ) ) );
Quadratic< SquareRoot > q3( 0, Functional< SquareRoot >( 0, SquareRoot( 5 ) ) );
q3 = q1 * (q1 + q2);
}
For more examples please see the Mean Median Map project.
|
| Conclusion |
|
The Proper Numbers Library is a small, efficient and fast set of C++ classes that allows representation of arbitrarily large integer numbers,
arbitrarily precise rational numbers, and irrational numbers. The library is very easy to integrate in any C++ project and be used as if the
classes defined in it were native for the language. Not all standard operators are defined in order to enforce stricter Object Oriented compliance
than the standard build in types. For example, the number classes have no implicit conversion to Boolean values. Besides, the standard arithmetic
operators that the classes have very few complex mathematical functions such as sine, cosine, roots, logarithm, etc, defined on them. However,
these can be easily added in future since all of these functions are constructed as series using the standard arithmetic operators. For the
most common uses, the classes offer the required functionality. In future, the library will be extended as required and appropriate. The problem
with the definition of the irrational number is also very interesting and hopefully will be addressed in the future with the required attention.
|
| Your Use Of The Proper Numbers Library In Your Projects |
The MIT Open Source License under which the library the is published allows you to use the library in any project, commercial or otherwise,
FREE of charge and FREE of any obligation, apart from the following two requirements:
1) To maintain the copyright and license notes on the top of each file as they are when you download them.
2) To place a note in the About/Help of your project that it is using the library. If it is possible to add a link to this page will be much appreciated.
|
Miroslav B. Bonchev
4-th May 2011
London, England |
How to Use the Proper Numbers Library
Download the Proper Numbers Library
|
|